티스토리 뷰
www.edwith.org/linearalgebra4ai/lecture/24798
[LECTURE] 그람-슈미트 직교화와 QR 분해 : edwith
학습목표 이번에는 임의의 행렬을 직교기저(Orthogonal basis)를 가지는 행렬로 변환하는 그람-슈미트 직교화에 대해 배워보겠습니다. 핵심 키워드 그람-슈미트 직교화(... - 커넥트재단
www.edwith.org
Gram-Schmidt Orthogonalization
행렬 \(A\)가 있습니다.
\(A = \begin{bmatrix} 3 && 1 \\ 6 && 2 \\ 0 && 2 \end{bmatrix} \)
\(A\)의 Column Vectors를 \(\mathbf{a}_{1}\), \(\mathbf{a}_{2}\)라고 정의하겠습니다. 이 Column Vectors는 Orthogonal 하지 않으며, 당연하게도 Orthonormal 하지 않습니다. 두 Column Vectors로 형성되는 Span을 해치지 않고 두 Column Vectors가 서로 Orthonormal 한 성질을 갖도록 변환시켜보겠습니다.
먼저, 하나의 벡터를 택하고 해당 벡터가 Normal Vector가 되도록 변환시킵니다. \(\mathbf{a}_{1}\)을 택하고 이 벡터의 Normal Vector \(\mathbf{u}_{1}\)라고 정의하겠습니다.
\(\mathbf{u}_{1} = \mathbf{v}_{1}/||\mathbf{v}_{1}||\)
이제 \(\mathbf{u}_{1}\)과 직교하는 Normal Vector \(\mathbf{u}_{2}\)를 구해야 합니다.

\(\mathbf{u}_{1}\)과 \(\mathbf{v}_{2}\)를 시각화 해보자면 위 그림 처럼 나타낼 수 있을 것입니다.(대충 그린 것이며 실제로 시각화를 해보면 저렇게 그려지지 않을 것입니다.)

\(\mathbf{v}_{2}\)를 \(\mathbf{u}_{1}\)에 정사영 내리고 정사영 내린 벡터를 \(\mathbf{v}_{2}\)에서 빼면 \(\mathbf{u}_{1}\)에 수직한 벡터를 구할 수 있습니다.
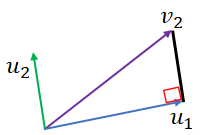
그리고, 그 수직한 벡터를 Normal Vector로 변환시켜주면 \(\mathbf{u}_{1}\)과 직교하는 Normal Vector \(\mathbf{u}_{2}\)가 나오게 됩니다.
\(A\)의 Column Vector가 하나 더 존재하는 경우를 생각해봅시다. 그리고, 그 벡터를 \(\mathbf{v}_{3}\)라고 하겠습니다.
\(\mathbf{v}_{3}\)를 \(\mathbf{u}_{1}\)에 대해 정사영 내리고 \(\mathbf{u}_{2}\)에 대해 정사영 내립니다. 정사영된 두 벡터를 \(\mathbf{v}_{3}\)에서 빼고, 그 벡터를 Normal Vector로 변환시켜주면 \(\mathbf{u}_{3}\)를 구할 수 있게 됩니다. 여기서, \(\mathbf{u}_{1}\) 과 \(\mathbf{u}_{2}\)는 서로 직교함에 주의합니다(추후 내용 보충).
QR Factorization
Gram-Schmidt Orthogonalization을 거쳐 어떤 행렬 \(A\)의 컬럼 벡터들이 Orthogonal 한 특성을 갖도록 변환 되었다고 가정해보겠습니다. 이 Orthogonal한 컬럼 벡터들에 대하여 Gram-Schmidt Orthogonalization 과정을 역으로 계산하면 \(A\)를 다시 구할 수 있습니다. 그리고 이 과정은 행렬 곱으로 표현이 가능합니다.
\(A = QR\)이라고 하였을때, 여기서 \(Q\)는 Gram-Schmidt Orthogonalization 과정을 통해 나온 Orthogonal Martrix입니다. \(R\)은 Orthogonal Matrix \(Q\)를 \(A\)로 복원하기위한 행렬로 해당 행렬은 Upper Triangular Matrix로 정의됩니다. 그리고 이러한 분해 과정을 QR Factorizaiton이라 합니다.
'Math > Linear Algebra' 카테고리의 다른 글
| 인공지능을 위한 선형대수 - CHAPTER 4.1 고유벡터와 고유값 (0) | 2021.01.24 |
|---|---|
| 인공지능을 위한 선형대수 - CHAPTER 3.5 Orthogonal Projection 2 (0) | 2020.12.27 |
| 인공지능을 위한 선형대수 - CHAPTER 3.4 Orthogonal Projection 1 (0) | 2020.12.08 |
| 인공지능을 위한 선형대수 - CHAPTER 3.3 정규방정식 (0) | 2020.11.14 |
| 인공지능을 위한 선형대수 - CHAPTER 3.2 Least Squares와 그 기하학적 의미 (0) | 2020.11.05 |
- Total
- Today
- Yesterday
- 백트래킹
- Lowest Common Ancestor
- 백준 1766
- 단축키
- 백준
- 인공지능을 위한 선형대수
- 백준 11437
- 조합
- 파이참
- MOT
- 자료구조
- 백준 11053
- 순열
- C++ Deploy
- 문제집
- ㅂ
- 위상 정렬 알고리즘
- PyCharm
- 이분탐색
- FairMOT
- 가장 긴 증가하는 부분 수열
- LCA
- cosine
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
