티스토리 뷰
www.edwith.org/linearalgebra4ai/lecture/24128/
[LECTURE] 전사함수와 일대일함수 : edwith
학습목표 이번 강의에서는 전사함수와 일대일함수를 배워보겠습니다. 그리고 이 개념이 실제로 Neural networks에는 어떻게 응용될 수 있는지를 생각해보는 시간을 갖겠습니다. ... - 커넥트재단
www.edwith.org
ONTO and ONE-TO-ONE
ONTO
전사함수(ONTO)는 공역(Co-domain) = 치역(Range)인 경우를 의미합니다.
Domain(정의역): Set of all the possible values of \(x\)
Co-domain(공역): Set of all the possible values of \(y\)
Image(상): a mapped output \(y\), given \(x\)
Range(치역): Set of all the output values mapped by each \(x\) in the domain
A mapping \(T : \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}\) is said to be onto \(\mathbb{R}^{m}\) if each \(\mathbf{b} \in \mathbb{R}^{m}\) is the image of at least one \(\mathbf{x} \in \mathbb{R}^{n}\).
That is, the range is equal to the co-domain.

ONTO가 되기 위해서 적어도 정의역의 Dimension이 공역의 Dimension보다 같거나 커야 합니다.
\(T : \mathbb{R}^{3} \rightarrow \mathbb{R}^{2}\)는 ONTO가 될 수 있지만, \(T : \mathbb{R}^{2} \rightarrow \mathbb{R}^{3}\)은 ONTO가 절대 될 수 없습니다.
Neural Networks에서 입력 벡터보다 출력 벡터의 차원이 큰 Layer 혹은 Network를 설계하는 경우가 존재합니다.

대표적으로 GAN의 Encoder/Decoder, AutoEncoder 구조를 생각해볼 수 있습니다.
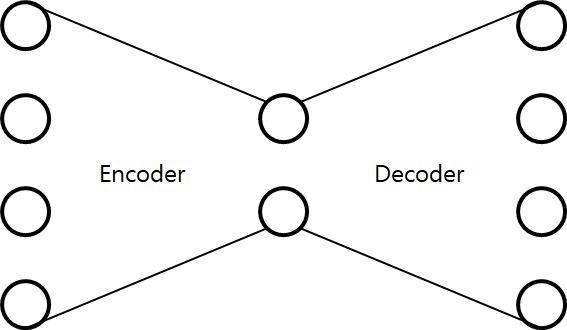
일반적으로 입력 벡터(\(\in \mathbb{R}^{n}\))보다 출력 벡터(\(\in \mathbb{R}^{m}\))의 차원이 더 큰(\( m > n \)) Layer들을 한데 묶어 Decoder라고 합니다. 그런데, 입력 벡터보다 출력 벡터의 차원이 더 큰 경우 ONTO가 될 수 없기 때문에 출력 벡터를 모두 커버할 수 없게됩니다. 하지만 몇몇 경우의 우리의 출력 벡터는 운이 좋게도 \(m\)차원의 공간상에서 \(m\)보다 작은 차원(3차원이였다면 2차원 평면)으로도 표현이 가능하게 됩니다.
ONE-TO-ONE
1대1 함수
A mapping \(T : \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}\) is said to be one-to-one if each \(\mathbf{b} \in \mathbb{R}^{m}\) is the image of at most one \(\mathbf{x} \in \mathbb{R}^{n}\). That is, each output vector in the range is mapped by only one input vector, no more than that.
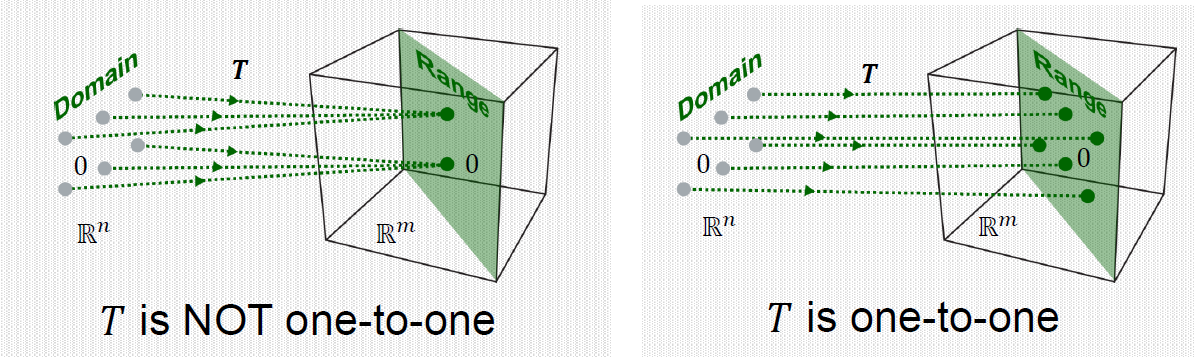
ONE-TO-ONE이 되기 위해서 적어도 정의역의 Dimension이 공역의 Dimension보다 같아야 합니다.
\(T : \mathbb{R}^{3} \rightarrow \mathbb{R}^{2}\)는 ONE-TO-ONE이 될 수 없지만, \(T : \mathbb{R}^{2} \rightarrow \mathbb{R}^{3}\)은 ONE-TO-ONE이 될 수 있습니다.
\(A \mathbf{x} = \mathbf{b}\) 일때, \(A\)가 Linearly Dependent하다면 정의역의 크기가 치역보다 커지게 됩니다. 즉, \(A \mathbf{x} = \mathbf{b}\)를 만족하는 \(\mathbf{x}\)의 갯수가 1개 이상으로 해당 Linear Transformation은 ONE-TO-ONE이 될 수 없습니다. 반대로, \(A\)가 Linearly Independent하다면 해당 Linear Transformation은 ONE-TO-ONE이 됩니다.
ONTO는 결국 MANY-TO-ONE으로도 생각할 수 있습니다. 입력 벡터와 출력 벡터간의 ONTO, ONE-TO-ONE 관계를 잘 생각해보면 Neural Network에서 Layer의 입력 벡터 및 출력 벡터의 차원 수에 따라 MANY-TO-ONE이 될 수 있을 것인지, ONE-TO-ONE이 될 수 있을 것인지를 예상해볼 수 있습니다.
'Math > Linear Algebra' 카테고리의 다른 글
| 인공지능을 위한 선형대수 - CHAPTER 3.2 Least Squares와 그 기하학적 의미 (0) | 2020.11.05 |
|---|---|
| 인공지능을 위한 선형대수 - CHAPTER 3.1 Least Squares Problem 소개 (0) | 2020.10.24 |
| 인공지능을 위한 선형대수 - CHAPTER 2.6 선형변환 with Neural Networks (0) | 2020.10.22 |
| 인공지능을 위한 선형대수 - CHAPTER 2.5 선형변환 (0) | 2020.10.20 |
| 인공지능을 위한 선형대수 - CHAPTER 2.4 부분공간의 기저와 차원 (0) | 2020.10.18 |
- Total
- Today
- Yesterday
- PyCharm
- ㅂ
- 위상 정렬 알고리즘
- FairMOT
- Lowest Common Ancestor
- 파이참
- 백준 11437
- 이분탐색
- 백준
- 가장 긴 증가하는 부분 수열
- 백준 1766
- C++ Deploy
- cosine
- 인공지능을 위한 선형대수
- 백준 11053
- LCA
- 조합
- 자료구조
- MOT
- 백트래킹
- 단축키
- 문제집
- 순열
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
