티스토리 뷰
https://www.acmicpc.net/problem/11053
11053번: 가장 긴 증가하는 부분 수열
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오. 예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이
www.acmicpc.net
본 문제는 주어진 수열로부터 가장 긴 증가하는 부분 수열의 크기를 계산하는 문제입니다.
해당 문제는 Longest Increasing Subsequence Problem 이라는 영명으로 존재하는 굉장히 유명한 알고리즘 문제였습니다.
저는 다이나믹 프로그래밍 기법을 사용하여 해당 문제를 풀었습니다.
예시를 들어 설명드리도록 하겠습니다.
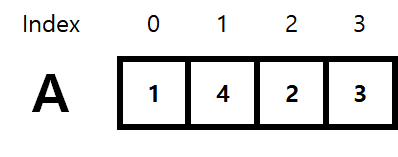
1, 4, 2, 3 의 값을 원소로 갖는 순열 A가 있습니다. 다음 그림을 보도록 하겠습니다.

그림에서 DP 란 Table 이 추가 되었습니다. DP[i] 의 의미는 A[:i+1] 의 원소들로 만들 수 있는 A[i] 를 포함하는 가장 긴 증가하는 부분 수열의 크기를 의미합니다. DP Table 밑에 존재하는 집합은 A[:i+1] 의 원소들로 만들 수 있는 A[i] 를 포함하는 가장 긴 증가하는 부분 수열을 나타냅니다. 해당 문제에서 가장 긴 증가하는 부분 수열의 원소들을 출력할 필요는 없으나 문제 설명을 돕기 위해 첨부하였습니다.
DP[1] 값을 구해보도록 하겠습니다.

DP[1] 값은 1입니다. DP[1] 을 구할때 우리는 A[:1] 의 원소들로 만들 수 있는 A[0]를 포함하는 가장 긴 증가하는 부분 수열에다 A[1] 을 삽입할 수 있는지 없는지(증가하는 부분 순열의 성질이 유지되는지)를 판단해서 삽입할 수 있다면 DP[0]+1 이 됩니다. A[1] 을 삽입할 수 없는 경우라면 크기가 1인 A[1] 만으로 이루어진 부분 수열을 만들 수 있으므로 DP[1]은 1이 됩니다.
DP[2] 값을 구해보도록 하겠습니다.

DP[2] 값은 2입니다. DP[2] 를 구할때 A[:1] 의 원소들로 만들 수 있는 가장 긴 부분 수열과 A[:2] 의 원소들로 만들 수 있는 가장 긴 부분 수열에 A[2]를 삽입할 수 있는지 없는지를 확인해주고 DP[2] 값을 업데이트 해주면 됩니다. 여기까지 설명을 읽고 이해가 되셨다면 규칙을 발견하셨을듯 합니다!
DP[i] 의 값은 A[:1], A[:2], ..., A[:i] 의 원소들로 만들 수 있는 i 개의 가장 긴 부분 수열들의 크기로부터 계산 될 수 있습니다.
DP[3] 값을 구해보도록 하겠습니다.

해당 알고리즘의 복잡도는 O(N^2) 입니다. 해당 문제는 유명한 문제이다 보니 보다 낮은 복잡도를 갖는 알고리즘도 찾을 수 있었습니다. 다음번에 유사 문제를 풀 기회가 있을때는 복잡도가 더 낮은 알고리즘을 설계하여 문제를 풀어보고 관련 글을 게시하도록 하겠습니다.
코드
#include <iostream>
#include <algorithm>
using namespace std;
int N;
int A[1000];
int dp[1000];// dp[i] = "i 번째 자리에 위치한 A[i]" 를 포함하는 가장 긴 증가하는 부분 수열의 수
int main()
{
cin >> N;
for(int i = 0; i < N; i++)
{
cin >> A[i];
}
for(int i = 0; i < N; i++)
{
dp[i] = 1;
for(int j = 0; j < i; j++)
{
if(A[j] < A[i])
{
dp[i] = max(dp[i], dp[j] + 1);
}
}
}
cout << *max_element(dp, dp + N);
return 0;
}'Problem Solving > 백준 온라인 저지' 카테고리의 다른 글
| 1793-타일링 (0) | 2020.09.11 |
|---|---|
| 3197-백조의 호수 (0) | 2020.09.11 |
| 1562-계단 수 (0) | 2020.09.07 |
| 11437-LCA (0) | 2020.09.02 |
| 1766-문제집 (1) | 2020.09.01 |
- Total
- Today
- Yesterday
- 백트래킹
- 이분탐색
- 조합
- MOT
- 백준 1766
- 위상 정렬 알고리즘
- 자료구조
- ㅂ
- 백준
- 단축키
- 파이참
- 문제집
- Lowest Common Ancestor
- cosine
- 백준 11437
- LCA
- 인공지능을 위한 선형대수
- PyCharm
- 백준 11053
- C++ Deploy
- 순열
- FairMOT
- 가장 긴 증가하는 부분 수열
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
